Recalc

Recalc is short for “recalculate”, and is basically the command that tells AnkiMorphs to work all its magic. When you run Recalc, AnkiMorphs will go through the cards that match any ‘Note Filter’ and do the following:

• Update the ankimorphs.db with any new seen morphs, known morphs, etc.
• Calculate the score of the cards, and then sort the cards based on that score.
• Update any cards’ extra fields and tags.

Basically, when you run Recalc, AnkiMorphs will go through your collection, recalculate the difficulty of your cards based on your new knowledge, and reorder your new cards in a way that’s optimal for the new you: the you who knows more than you did yesterday.

You can run Recalc as often as you like, but you should run it at least once before or after every study session so that your new cards will appear in the optimal order.

It’s easy to forget to run recalc, so you can also check the Recalc on sync settings option, which will take care of recalc for you by running it automatically before Anki syncs your collection.

Note: Recalc can potentially reorganize all your cards, which can cause long sync times. The Anki FAQ has some tricks you can try if this poses a significant problem.

Scoring Algorithm

TL;DR: Low scores are good, high scores are bad.

The order in which new cards are displayed depends on their due value: a card with due = 1 will be shown before a card with due = 2, and so on. Leveraging this property, we can implement the following strategy: assign higher due values to cards with more complex text, pushing them further back in the card queue. Here are some examples of what that might look like:

• “She walked home”
  • due = 600
• “Asymmetric catalysis for the enantioselective synthesis of chiral molecules”
  • due = 100 000 000

Now, let’s define some properties that we want our cards to have:

• Few unknowns morphs (comprehensibility)
• High priority morphs (significance)
• Ideal length (low deviation)

We can now invert these properties to calculate a “penalty” score, which will then replace the due values of the cards. That formula at the highest level is:

\[ \large \text{score} = \text{incomprehensibility} + \text{insignificance} + \text{deviation} \]

Let’s break it down into smaller components.

incomprehensibility

In practice, the comprehensibility of a given text is determined by a combination of known grammar points and vocabulary. However, evaluating grammar is non-trivial, especially in a general language learning context, so we will not make any explicit attempts to do so.

Determining which morphs are known is relatively easy, so our incomprehensibility score will be the product of the number of unknown morphs and a constant penalty factor.

\[ \large \text{incomprehensibility} = PU \times \left| M_{\text{U}} \right| \]

where \[ {\large \begin{align*} & PU: \text{penalty for unknown} = 10^6\\ & M: \text{set of identified morphs} \\ & m_{\text{li}}: \text{morph learning interval} \\ & M_U: \text{unknown morphs} = { m \in M \mid m_{\text{li}} = 0 } \\ \end{align*} } \]

insignificance

Each morph has a priority value, which AnkiMorphs aggregates into the following metrics: \[ {\Large \begin{array}{ccc} \begin{aligned} \\[15pt] P_{\text{total}}^{\text{all}} &= \sum_{m \in M}{m_p} \\[20pt] P_{\text{total}}^{\text{unknown}} &= \sum_{m \in M_{\text{U}}}{m_p} \\[20pt] P_{\text{total}}^{\text{learning}} &= \sum_{m \in M_{\text{L}}}{m_p} \\ \end{aligned} & & \begin{aligned} \\[1pt] P_{\text{average}}^{\text{all}} &= \frac{P_{\text{total}}^{\text{all}}}{\left| M \right|} \\[20pt] \\[25pt] P_{\text{average}}^{\text{learning}} &= \frac{P_{\text{total}}^{\text{learning}}}{\left| M_{\text{L}} \right|} \ \end{aligned} \end{array} } \]

where \[ {\large \begin{align*} & m_{\text{p}}: \text{morph priority} \\ & M_{\text{L}}: \text{learning morphs} = { m \in M \mid 0 < m_{\text{li}} < \text{known threshold} } \\ \end{align*} } \]

Note: \(\large P_{\text{average}}^{\text{unknown}}\) is not included since it would not have any meaningful impact on 1T cards.

You can customize the algorithm by selecting any combination of these metrics and adjusting their influence on the result by changing their corresponding weights. This is done using two column vectors: one for the weights and one for the aggregated metrics. The final score is computed by taking the scalar product of these vectors:

\[ {\large \mathbf{W_P} = \begin{pmatrix} \begin{array}{l} W_{\text{total}}^{\text{all}} \\[10pt] W_{\text{total}}^{\text{unknown}} \\[10pt] W_{\text{total}}^{\text{learning}} \\[10pt] W_{\text{average}}^{\text{all}} \\[10pt] W_{\text{average}}^{\text{learning}} \\[10pt] \end{array} \end{pmatrix} \quad \mathbf{P} = \begin{pmatrix} \begin{array}{l} P_{\text{total}}^{\text{all}} \\[10pt] P_{\text{total}}^{\text{unknown}} \\[10pt] P_{\text{total}}^{\text{learning}} \\[10pt] P_{\text{average}}^{\text{all}} \\[10pt] P_{\text{average}}^{\text{learning}} \\[10pt] \end{array} \end{pmatrix} } \]

which gives us: \[ \large \text{insignificance} = W_P \cdot P = w_1 p_1 + w_2 p_2 + \cdots + w_n p_n = \sum_{i=1}^{n} w_i p_i \]

Example:

\[ {\large \mathbf{W_P} = \begin{pmatrix} \begin{array}{c} 10 \\[10pt] 0 \\[10pt] 0 \\[10pt] 0 \\[10pt] 5 \\[10pt] \end{array} \end{pmatrix} \quad \mathbf{P} = \begin{pmatrix} \begin{array}{c} 600 \\[10pt] 30 \\[10pt] 20 \\[10pt] 100 \\[10pt] 10 \\[10pt] \end{array} \end{pmatrix} } \]
\[ \large W_P \cdot P = 10 \times 600 + 0 \times 30 + 0 \times 20 + 0 \times 100 + 5 \times 10 = 6050 \]

Deviation

Learning can be easier with more surrounding context, e.g., other known words. However, if a sentence contains too many words, learning may become more challenging. This is because the complexity of the grammar often increases, along with the likelihood of not perfectly remembering all the surrounding words. Ideally, we want our cards to have sentences within this optimal range.

Having the ability to bias our sentences towards a certain length is also beneficial; you might find it easier to learn from shorter sentences compared to longer ones, or vice versa.

To achieve this, we use a piecewise equation that where we define the following:

• How much to penalize excessive morphs
• How much to penalize insufficient morphs
• The ideal range (target) of morphs

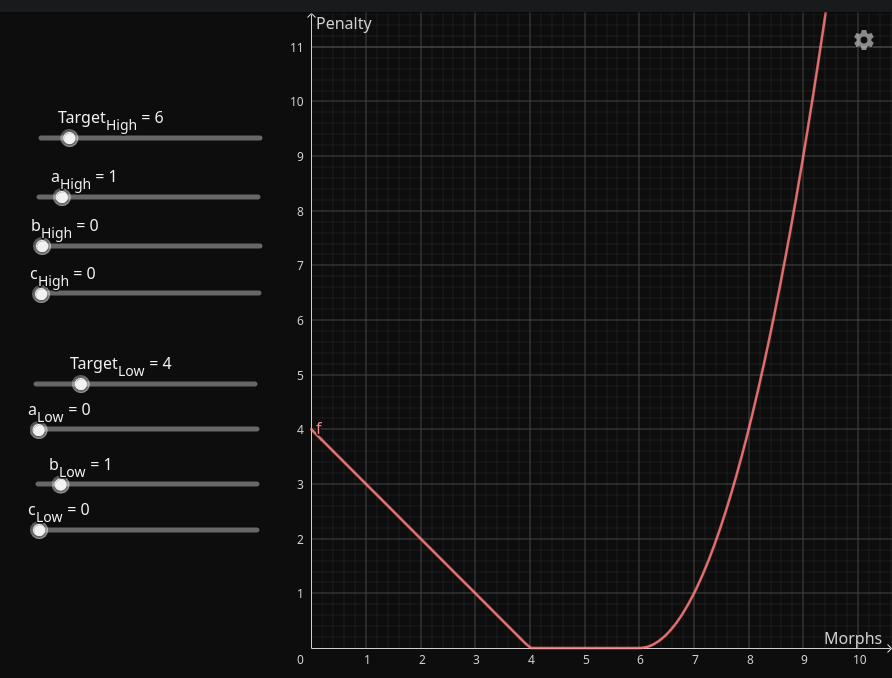
Here is an example of what that might look like:

Playground: https://www.geogebra.org/graphing/ta3eqb8y

This graph shows:

• Penalty for excessive morphs: squared in relation to the target difference
• Penalty for insufficient morphs: linear in relation to the target difference
• Ideal range (target): 4-6 morphs

AnkiMorphs provides the following metrics, which you can influence by changing the coefficients:

\[ {\large D_{\text{target}}^{\text{all}} = \begin{cases} \lceil a_H (|n - T_H|^2) + b_H |n - T_H| + c_H\rceil & \text{if } n > T_H \\ \lceil a_L (|n - T_L|^2) + b_L |n - T_L| + c_L\rceil & \text{if } n < T_L \\ 0 & \text{otherwise} \end{cases} } \]

\[ {\large D_{\text{target}}^{\text{learning}} = \begin{cases} \lceil a_H (|n_L - T_H|^2) + b_H |n_L - T_H| + c_H\rceil & \text{if } n_L > T_H \\ \lceil a_L (|n_L - T_L|^2) + b_L |n_L - T_L| + c_L\rceil & \text{if } n_L < T_L \\ 0 & \text{otherwise} \end{cases} } \]

where \[ {\large \begin{align*} & D_{\text{target}}: \text{target difference} \\ & \lceil \; \rceil: \text{round up to the nearest integer} \\ & T_H: \text{high target} \\ & T_L: \text{low target} \\ & n: \text{number of morphs} = \left| M \right|\\ & n_L: \text{number of learning morphs} = \left| M_{\text{L}} \right| \\ & a_H, b_H, c_H : \text{coefficients when \( n \) or \( n_L \) is greater than \( T_H \)} \\ & a_L, b_L, c_L : \text{coefficients when \( n \) or \( n_L \) is less than \( T_L \)} \\ \end{align*} } \]

with the following vectors:

\[ {\large \mathbf{W_D} = \begin{pmatrix} \begin{array}{l} W_{\text{target}}^{\text{all}} \\[10pt] W_{\text{target}}^{\text{learning}} \\[10pt] \end{array} \end{pmatrix} \quad \mathbf{D} = \begin{pmatrix} \begin{array}{l} D_{\text{target}}^{\text{all}} \\[10pt] D_{\text{target}}^{\text{learning}} \\[10pt] \end{array} \end{pmatrix} } \]

which gives us: \[ \large \text{deviation} = W_D \cdot D = \sum_{i=1}^{n} w_i d_i \]

Constraints

We have now refined the formula to:

\[ {\large \begin{align*} \text{score} &= \text{incomprehensibility} + \text{insignificance} + \text{deviation}\\ \text{score} &= PU \times \left| M_{\text{U}} \right| + W_P \cdot P + W_D \cdot D \end{align*} } \]

However, there are a few practical concerns we have to address.

First, we need to ensure that cards are primarily ordered by the number of unknown morphs they contain. This means that all 1T cards should appear before any MT cards, regardless of their insignificance or deviation.

To do this, we apply a min function to ensure that the sum of the last two terms does not exceed \(PU - 1\) \[ \large \text{score} = PU \times \left| M_{\text{U}} \right| + \min \left(W_P \cdot P + W_D \cdot D,\ PU - 1\right) \]

where \[ {\large \begin{align*} & \min: \text{choose the side that has the smallest number} \ \end{align*} } \]

Lastly, we have to make sure that the score does not exceed the maximum card due value allowed by Anki. The due value is stored as a signed 32-bit integer, with a maximum value of \(2^{31} - 1\). To prevent overflow when cards are shifted, we include a safety margin of \(10^8\). This results in the upper bound:

\[ \large \text{score}_{\text{max}} = 2^{31} - 1 - 10^8 \]

Now we wrap the entire expression in another min function to get our final formula:

\[ \large \text{score} = \min \left(PU \times \left| M_{\text{U}} \right| + \min \left(W_P \cdot P + W_D \cdot D,\ PU - 1\right),\ \text{score}_{\text{max}} \right) \]